Skilltest in Statistics – Solutions

Introduction
Statistics is one of the founding pillars for a career in data science and business analytics. Unless a person understands the basics of statistics well, he will not be able to perform well in data science. We launched Statistics skill test to help our community with a tool to assess their skills in statistics. You can look at the leaderboard of the skill assessment platform here
More than 1800 people registered on the hackathon and 533 people actually assessed themselves in 2 hours.
For all those who could not attend the skill assessment, check out how many questions you can answer correctly. I am sure you will take away learning points form this article and improve your knowledge about statistics.
For those who enjoyed the experience and would want to undergo this again on a more advanced topic, here is your chance to register in Statistics Skill Test – 2 . Also, check out our skill test on R.
Overall Results
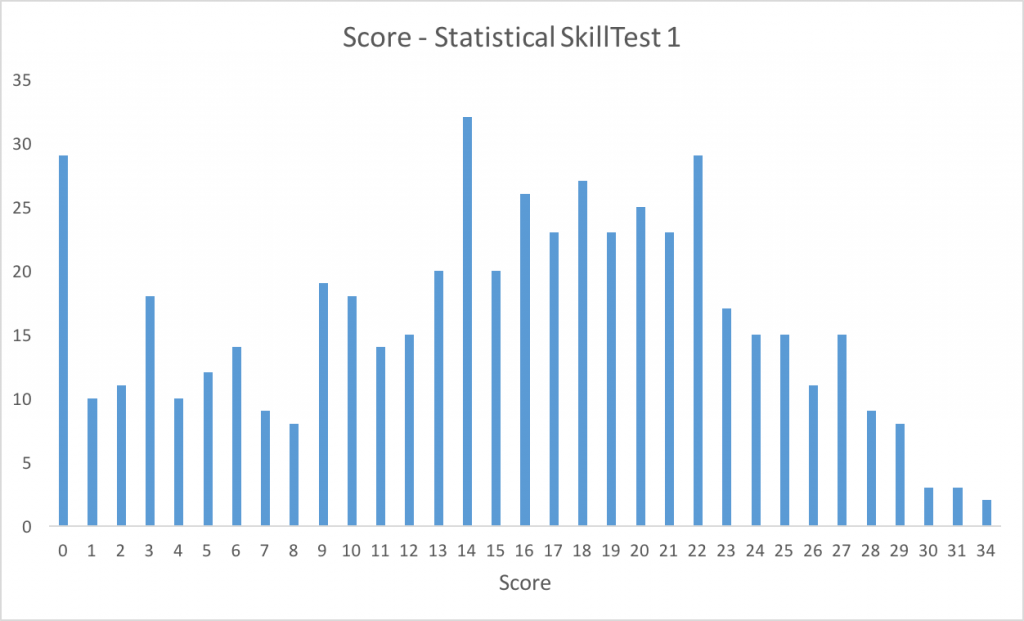
Who could have asked for a better way to analyze the results of a statistical skill test on this topic? Here is the distribution of the scores:
Here are a few measures of the distribution:
Mean = 14.99
Median = 16
Mode = 14
Let us look at the variance:
Standard Deviation = 8.13
95% confidence interval – [0, 30.94)
So, congratulations for the top 5 people (31 and above) to set themselves above the rest of the population.
If your score is more than 21, you are in the top 25 percentile – you deserve a pat!
On the other hand, people with score less than 9 probably need to spend more time on these concepts – believe me, it wasn’t tough!
Skill Test Questions and Answers
The skill test consisted of 40 questions selected very carefully based on the concepts which we think any individual pursuing a career in analytics should have them on their tips.
Read on to find out detailed solution of the all the questions.
1) Which measure of central tendency describes the following right-skewed distribution in the best manner?
a)Mean
b)Median
c)Mode
d)All of these
Ans: b) Median
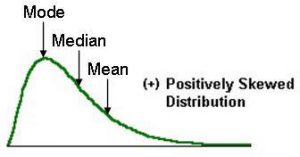
In skewed distributions, the mean will be in one extreme(towards the skew) and mode on the other. Whereas the median lies in the centre.
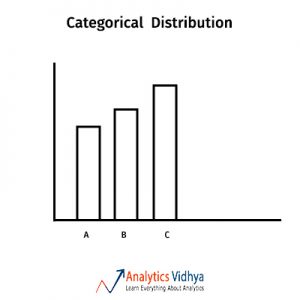
2) Which measure of central tendency describes the following nominal/categorical distribution in the best manner?
a)Mean
b)Median
c)Mode
d)All of these
Ans: c) Mode
Mean and median don’t make sense in categorical distributions. So mode describes central tendency at best.
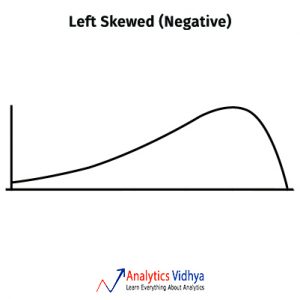
3) Which measure of central tendency describes the following left-skewed distribution in the best manner?
a)Mean
b)Median
c)Mode
d)All of these
Ans: b) Median
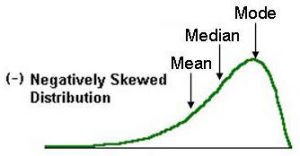
In skewed distributions the mean will be in one extreme(towards the skew) and mode in the other. Whereas the median lies in the centre.
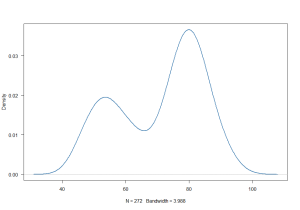
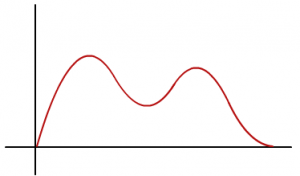
4) Which measure of central tendency suits the best for this bi-modal distribution?
a)Mean
b)Median
c)Mode
d)Mean or Median
Ans: b) Median
In Bimodal distributions, if distribution is symmetric then mean or median could be the representative for Central tendency whereas in this case due to skewness which can be clearly seen in the image, the mode lies at the left ‘bump’ and the mean lies close to the left ‘bump’ too(due to the left skew). Whereas the median should lie fairly at the centre.
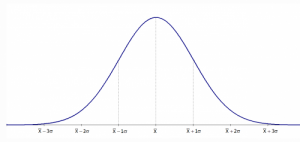
5) Which measure of central tendency suits the best for a normal distribution?
a)Mean
b)Median
c)Mode
d)All of these
Ans: d) All of these
Mean = Median = Mode for a normal distribution, as evident in the image.
6) Which of the following distribution satisfy the following relationship: Mode > Median > Mean?
a)Positive skewed
b)Negative skewed
c)Normal
d)Bi-modal
Ans: b) Negatively skewed

In skewed distributions the mean will be in one extreme(towards the skew) and mode in the other. Whereas the median lies in the centre. In this case mean lies towards the left(the skew).
Read more for a detailed explaination.
7) Which of the following distribution satisfy the following relationship: Mode < Median < Mean?
a)Positive skewed
b)Negative skewed
c)Normal
d)Bi-modal
Ans: a) Positively skewed
In skewed distributions the mean will be in one extreme(towards the skew) and mode in the other. Whereas the median lies in the centre. In this case mean lies towards the right(the skew).
Read more for a detailed explaination.
8) Which of the following distribution can satisfy the following relationship: Mode > Median > Mean?
a)Normal
b)Bi-modal
c)Uniform
d)None of these
Ans: b) Bi-modal
Imagine a bi-modal distribution with the mode in the right ‘bump’. The relation satisfies in such a distribution.
9) Which of the following operation reduces skewness in a Negatively skewed distribution in the best manner?
a)log
b)square
c)square root
d)skewness isn’t reducible property
Ans: b) Square
Any reducible function(in this case log and sqrt) will increase the skew as the values will be pushed to the left. Hence square is the only possible option.
Read more for detailed explaination.
10) Which of the following operation reduces skewness in a Positively skewed distribution?
a)log
b)square
c)square root
d)Skewness isn’t reducible property
Ans: a) log
In case of positive skew we need to scale the values towards the left to reduce skewness. So any reducible function would suffice(in this case log or sqrt). We can’t conclusively say which of the functions work better without knowing the actual distribution.
11) Which of these is not a measure of Variability?
a)Inter Quartile Range
b)Variance
c)Range
d)Median
Ans: d) Median
Median is a measure of Central tendency whereas others measure Variability / spread.
12) To quantify spread/variability a reasonable estimate of Variance can be calculated by averaging.
a)squared error
b)absolute error
c)Errors^4
d)a & b
Ans: d) A & B
It is only a matter of convenience on using either of the two. Sometimes people use absolute error and sometimes the square errors depending on their requirement.
Read more for your better understanding.
13) Why can’t Errors^4 be averaged to calculate Variance?
a)As per definition
b)because of heavy weightage to outliers
c)Gives similar results like squared errors
d)Computationally expensive
Ans: b) because of heavy weightage to outliers
Our objective is to quantify spread, that is how far each point is from the mean. Sum of Errors^4 will increase the errors due to outliers substantially and overestimate Variance. Hence we avoid it.
14) Why is error squared to calculate variance/S.D.?
a)By definition of variance
b)So that positive – negative errors don’t cancel out
c)Empirical evidence shows that it’s the best estimate
d)None of These
Ans: b) So that positive – negative errors don’t cancel out
Our objective is to quantify spread, that is how far each point is from the mean. To compute how ‘far’ we need to ensure that errors don’t cancel out. Hence we square or take the absolute and then compute average.
15) Which of these is not possible (Numerically)?
a)Mean > Variance > Standard Deviation
b)Variance > Standard deviation > Mean
c)Mean > Standard Deviation > Variance
d)None of these
Ans: d) None of these
All are possible. For Variance > 1, Variance is always greater than Standard Deviation. So a) and b) are possible(imagine a normal distribution with a large mean and negative mean respectively). c) is possible for Variance < 1 and a Mean > 1. So d) is the answer.
16) Which of the following is the best point estimate for population mean?
a)Sample mean
b)Sample mean/root(n-1)
c)Sample median
d)Sample median/root(n-1)
Ans: a) Sample Mean
Expected value(Sample Mean) = Population Mean
17) Which of the following is the best point estimate for population standard deviation?
a)Sample standard deviation
b)sqrt(Sum of squared errors/n-1)
c)sqrt(Sum of squared errors/n)
d)None of These
Ans: b) sqrt((Sum of squared errors)/(n-1)))
Expected value(sqrt((Sum of squared errors)/(n-1))) = Population Standard Deviation
This is called Bessel’s correction.
Read more for better understanding.
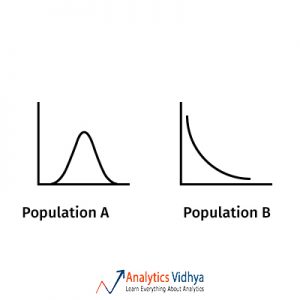
18) Population ‘A’ has a normal distribution and Population ‘B’ has an exponential distribution. The sampling distribution of sample means(large sample size) of both A and B are
a)Both Exponential
b)Normal for A and Exponential for B
c)Exponential for A and Normal for B
d)Both Normal
Ans: d) Both Normal
Central Limit theorem say that the sampling distribution of sample means for a large enough sample from any distribution follows a normal distribution.
19) Since the population size is always greater than the sample size, which of the following is true ?
a)the sample parameter can never be equal to the population parameter
b)The sample parameter can never be greater than the population parameter
c)The sample parameter can never be lesser than the population parameter
d)None of these
Ans: d) None of these
Depending on what sample has been drawn from the population, the statistic can be greater, lesser or equal to the population parameter.
20) Population ‘A’ has a normal distribution and population ‘B’ has an exponential distribution. The z distributions of both A and B is ?
a)the sample parameter can never be equal to the population parameter
b)The sample parameter can never be greater than the population parameter
c)The sample parameter can never be lesser than the population parameter
d)None of these
Ans: d) The same normal distribution
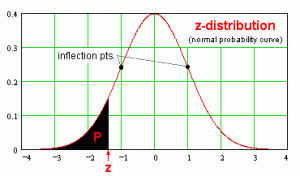
The z-distribution is one absolute normal distribution with mean 0 and standard deviation 1.
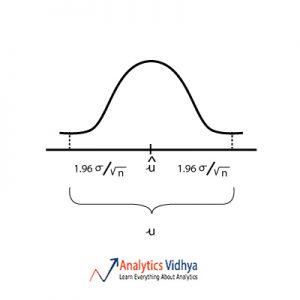
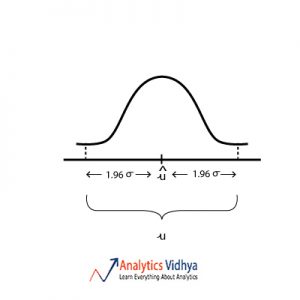
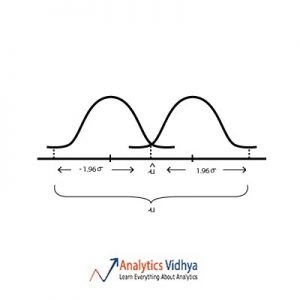
21) Which diagram best represents u (point estimate), û (population mean), σ (population standard deviation) for approximately 95 percent confidence interval ?
Ans:
a)
b)
c)
d)
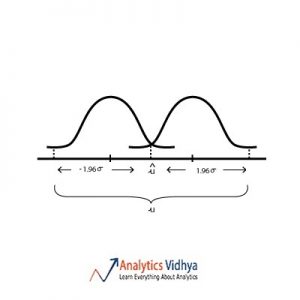 When we estimate population mean from sample mean we assume that sample mean lies within the 95% interval of the sampling distribution. Watch the below video to get a better understanding.
When we estimate population mean from sample mean we assume that sample mean lies within the 95% interval of the sampling distribution. Watch the below video to get a better understanding.
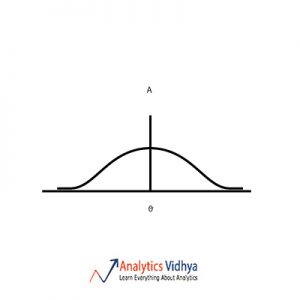
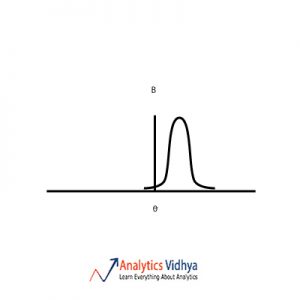
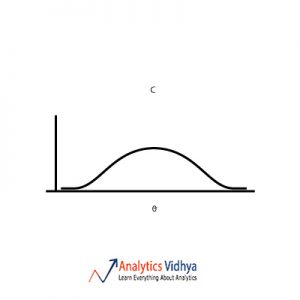
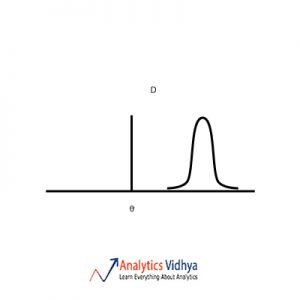
22) Which is the best point estimate among the A, B, C & D (given are the frequency plots for each point estimate and Θ is the population parameter we are trying to estimate) ?
Ans: b)
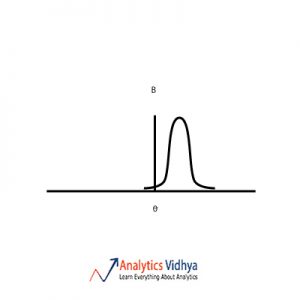 The point estimate should have low bias and low variance. Option a) has zero bias and high variance. Option b) has low bias and low variance. Option c) has high variance and high bias.
The point estimate should have low bias and low variance. Option a) has zero bias and high variance. Option b) has low bias and low variance. Option c) has high variance and high bias.
Option d) has high bias and low variance. So we go with Option b).
23) Suppose I say “The population parameter lies in 80% confidence interval (100, 200).” What is the confidence level?
a)20%
b)95%
c)80%
d)50%
Ans: c) 80%
Confidence level is how confident we are on the confidence interval, so 80%.
24) A group of students were surveyed on whether they skip breakfast or not. The 95% confidence interval was found to be (0.20, 0.27). Which of the following is the correct interpretation of the 95% confidence interval ?
a)There is a 95% probability that the proportion of young adults who skip breakfast is between 0.20 and 0.27
b)If this study were to be repeated with a sample of the same size, there is a 95% probability that the sample proportion would be between 0.20 and 0.27.
c)We can be 95% confident that the sample proportion of young adults who skip breakfast is between 0.20 and 0.27
d)We can be 95% confident that the population proportion of young adults who skip breakfast is between 0.20 and 0.27.
Ans: d) We can be 95% confident that the population proportion of young adults who skip breakfast is between 0.20 and 0.27
By definition of Confidence interval d) suits the best. Read more for better understanding.
25) What is the relationship between ‘significance level’ and ‘confidence level’?
a)Significance level = Confidence level
b)Significance level = 1 – Confidence level
c)Significance level = 1/Confidence level
d)Significance level = sqrt(1-Confidence level)
Ans: b) Significance level = 1 – Confidence level
If alpha equals 0.05, then your confidence level is 0.95. If you increase alpha, you both increase the probability of incorrectly rejecting the null hypothesis and also decrease your confidence level. ‘alpha’ is synonymous with Significance level.
Read more for better understanding.
26) The distribution of ‘number of travels per year’ is normal with a mean of 50 and a standard deviation of 8. Which option describes how to find the proportion of people that have a number of travels greater than 58?
a)Find the area to the left of z = 1 under a standard normal curve.
b)Find the area between z = -1 and z = 1 under a standard normal curve.
c)Find the area to the right of z = 1 under a standard normal curve.
d)Find the area to the right of z = -1 under a standard normal curve.
Ans: c) Find the area to the right of z = 1 under a standard normal curve
 The z-value can be calculated to be 1. We are looking at proportions which have values greater than the given value as shown below.
The z-value can be calculated to be 1. We are looking at proportions which have values greater than the given value as shown below.
27) A sample of 400 students from a university were randomly selected. They were asked if the current duration of the university needed to be reduced. 46% of the students, answered yes. Which one of the following statements about the number 46% is correct?
a)It is a sample statistic
b)It is a population parameter.
c)It is a margin of error
d)it is a standard error
Ans: a) It is a sample statistic
400 is the sample size and 46% is the measure calculated on that sample otherwise known as ‘sample statistic’.
28) A sample of 400 students from a university were randomly selected. They were asked if the current duration of the university needed to be reduced. 46% of the students, answered yes. What is the standard error of the sample proportion of students who answered yes to the question?
a) 0.249
b)0.0249
c) 0.498
d) 0.0498
Ans: b) 0.0249
SE of proportion = sqrt [ p(1 – p) / n ], applying the above formula we can calculate the SE to be 0.0249. Read more for better understanding.
29) A sample of 400 students from a university were randomly selected. They were asked if the current duration of the university needed to be reduced. 46% of the students, answered yes. If the sample proportion of students who answered yes to the question was 26% instead of 46%, the margin of error would be?
a) smaller
b) larger
c) same
d)Can’t determine
Ans: a) smaller
Margin of error = 2*SE of proportion = 2*sqrt [ p(1 – p) / n ]. Calculating Margin of error for both 26% and 46% we find that Margin of error of 26% to be smaller than that of 46%. Read more for better understanding.
30) A sample of 400 students from a university were randomly selected. They were asked if the current duration of the university needed to be reduced. 46% of the students, answered yes. If the sample consisted of 300 students instead of 400 students, but the sample proportion of students who answered yes to the question was still 46%, the margin of error would be ?
a) smaller
b) larger
c) same
d)Can’t determine
Ans: b) larger
Margin of error = 2*SE of proportion = 2*sqrt [ p(1 – p) / n ]. Calculating Margin of error for both sample sizes (n = 400 and n = 300) find that Margin of error of n = 300 to be larger than that of n = 400. Read more for detailed explaination.
31) The 95% Confidence interval of population mean is calculated from a sample. If a few outliers are added to the sample the new 95% Confidence interval would be ?
a) wider
b) thinner
c) same
d)Insufficient data
Ans: a) Wider
Confidence interval = (sample mean – Margin of error, sample mean + Margin of error). The size of the interval is determined by Margin of error. Margin of error = 2 * Standard error, Standard error = Standard deviation/sqrt(n). Adding outliers will increase the standard deviation which will increase the standard error which again will in turn increase the margin of error, thus making the interval wider.
32) For a population with standard deviation = 7, a sample of 9 elements was chosen arbitrarily. The sample mean was found out to be equal to 56. Calculate the margin of error assuming 95% confidence interval.
a)6.79
b)5.25
c)4.57
d)5.33
Ans: c) 4.57
Margin of error = 2 * Standard error, Standard error = Standard deviation/sqrt(n). Applying the formula gives 4.57 as the Margin of error.
33) For a population with standard deviation = 7, a sample of 9 elements was chosen arbitrarily. The sample mean was found out to be equal to 56. Assuming that the sample mean lies in the margin of error, the 95% confidence interval in which population mean lies is given by ?
a)(51.43, 60.57)
b)(49.21, 62.79)
c)(50.67, 61.33)
d)(50.75, 61.25)
Ans: a) (51.43, 60.57)
Confidence interval = (sample mean – 2*Standard error, sample mean + 2*Standard error)
Read more for further explaination.
34) Find the minimum confidence level for which population mean of 60 lies within the confidence interval of sample (sample mean = 54, standard deviation of the population = 10 and the size of sample = 25).
a) 95%
b)98.67%
c)99.87%
d)99.92%
Refer to the z-table and t- table.
Ans: c) 99.87%
z = (x – u)/sigma
Calculating z-value and referring to the z-table we get c). Read more for further explaination.
35) A 95% confidence interval was computed to be 0.20 to 0.27. From the information provided, we can determine that (where, û = sample mean, u = population mean) ?
a)û = 0.235 and margin of error = 0.035
b)û = 0.235 and margin of error = 0.07
c)u = 0.235 and margin of error = 0.035
d)u = 0.235 and margin of error = 0.07
Ans: a) û = 0.235 and margin of error = 0.035
Confidence interval = (sample mean – Margin of error, sample mean + Margin of error). From the above formula we obtain a). Read more for further explaination.
36) From a sample the 95% confidence interval is already computed. What is the probability that the population parameter lies in the interval?
a)0.95
b)0.5
c)0.05
d)None of these
Ans: b) 0.5
This is a tricky question which requires a comprehensive explanation. The ‘misunderstandings’ section in Wikipedia has a good explanation. Read more for detailed explaination.
37) A random sample of 1000 people is taken from a population of over a billion, in order to compute a confidence interval for some proportion. If the researchers wanted to decrease the width of the confidence interval, they could ?
a)decrease the size of population
b)decrease the size of sample
c)increase the size of population
d)increase the size of sample
Ans: d) increase the size of sample
Confidence interval = (sample mean – Margin of error, sample mean + Margin of error). The size of the interval is determined by Margin of error. Margin of error = 2 * Standard error, Standard error = Standard deviation/sqrt(n).
38) Suppose that a 95% confidence interval for the proportion of students at a school who played cricket is 35%± 5%. The confidence level is ?
a)5%
b)35%
c)95%
d)None of These
Ans: c) 95%
Confidence level is the measure of confidence on the computed interval, which implies that confidence level is 95%
39) Suppose that a 95% confidence interval for the proportion of students at a school who played cricket is 35% plus or minus 5%. The margin of error is ?
a)10%
b)5%
c)35%
d)95%
Ans: b) 5%
Confidence interval = (sample mean – Margin of error, sample mean + Margin of error). Hence b).
40) Suppose that a 95% confidence interval for the proportion of students at a school who played cricket is 35% plus or minus 5%. The 95% confidence interval for the proportion of students playing cricket is ?
a)10%
b)5%
c)35%
d)95%
Ans: d) 30% to 40%
Confidence interval = (sample mean – Margin of error, sample mean + Margin of error). Hence d).
This article taken from http://analyticsvidhya.com

Kalyan Banga226 Posts
I am Kalyan Banga, a Post Graduate in Business Analytics from Indian Institute of Management (IIM) Calcutta, a premier management institute, ranked best B-School in Asia in FT Masters management global rankings. I have spent 14 years in field of Research & Analytics.








0 Comments