By: Vikash Singh

Introduction

Employee Attrition is a challege for most of the organizations. More often than not, it’s a chellenge identifying variables or factors which may increase the probability of attrition as many of these are qualitative in nature. Even if one identifies these triggers, its difficult to quantify them and create a High- Medium – Low Risk Profile of the candidates. This is where Predictive Modeling can be of great help, and that is what is covered in the article.

Data

The dataset consists of 1470 observations of 15 variables which are described below:

• Attrition: Whether the attrition happened (Yes=1) or not (No=0). This is our independent variable which we are trying to score.
• Age
• BusinessTravel: relates to travel frequency of the employee
• Satisfaction_level: relates to environment satisfaction level of the employee (1-Low, 2-Medium, 3-High, 4-Very high)
• Sex – gender of the employee
• JobInvolvement: relates to job involvement level of the employee (1-Low, 2-Medium, 3-High, 4-Very high)
• JobSatisfaction: relates to job satisfaction level of the employee (1-Low, 2-Medium, 3-High, 4-Very high)
• MaritalStatus
• MonthlyIncome
• NumCompaniesWorked: how many companies has the employee worked upon
• OverTime: whether the employee works overtime (Yes / No)
• TrainingTimesLastYear: number of trainings received by the employee last year
• YearsInCurrentRole: number of years in current role
• YearsSinceLastPromotion: number of years since last promotion
• YearsWithCurrManager: number of years with current manager

Loading the Data

Data Exploration

1) Structure of the Data

str(attrition)

## ‘data.frame’:                                            1470 obs. of  15 variables:
##  $ Age                                                         : int  40 48 36 32 26 31 58 29 37 35 …
##  $ Attrition                                                : int  1 0 1 0 0 0 0 0 0 0 …
##  $ BusinessTravel                                 : Factor w/ 3 levels “Non-Travel”,”Travel_Frequently”,..: 3 2 3 2 3 2 3 3 2 3 …
##  $ Satisfaction_level                              : int  2 3 4 4 1 4 3 4 4 3 …
##  $ Sex                                                            : Factor w/ 2 levels “Female”,”Male”: 1 2 2 1 2 2 1 2 2 2 …
##  $ JobInvolvement                                : int  3 2 2 3 3 3 4 3 2 3 …
##  $ JobSatisfaction                                  : int  4 2 3 3 2 4 1 3 3 3 …
##  $ MaritalStatus                                     : Factor w/ 3 levels “Divorced”,”Married”,..: 3 2 3 2 2 3 2 1 3 2 …
##  $ MonthlyIncome                                : int  5394 4617 1881 2618 3121 2761 2403 2424 8573 4713 …
##  $ NumCompaniesWorked               : int  8 1 6 1 9 0 4 1 0 6 …
##  $ OverTime                                              : Factor w/ 2 levels “No”,”Yes”: 2 1 2 2 1 1 2 1 1 1 …
##  $ TrainingTimesLastYear                 : int  0 3 3 3 3 2 3 2 2 3 …
##  $ YearsInCurrentRole                       : int  4 7 0 7 2 7 0 0 7 7 …
##  $ YearsSinceLastPromotion           : int  0 1 0 3 2 3 0 0 1 7 …
##  $ YearsWithCurrManager              : int  5 7 0 0 2 6 0 0 8 7 …

#Converting categorical variables as factors which are coded as numbers
attrition$Attrition = as.factor(attrition$Attrition)
attrition$Satisfaction_level = as.factor(attrition$Satisfaction_level)
attrition$JobInvolvement = as.factor(attrition$JobInvolvement)
attrition$JobSatisfaction = as.factor(attrition$JobSatisfaction)

2) Missing Values

table(is.na(attrition))

##
## FALSE
## 22050

There are no missing values in the data set.

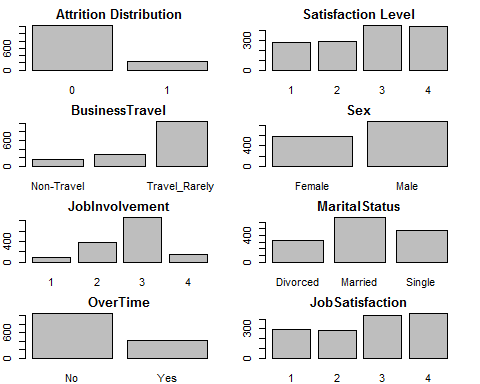
3) Visualisation of Independent Variables

For numerical variables, we will use histograms; whereas for Categorical Values, we will use Bar Charts or Frequency Counts.

Distribution of Categorical Variables

par(mfrow=c(4,2))
par(mar = rep(2, 4))
barplot(table(attrition$Attrition), main =“Attrition Distribution”)
barplot(table(attrition$Satisfaction_level), main =“Satisfaction Level”)
barplot(table(attrition$BusinessTravel), main =“BusinessTravel”)
barplot(table(attrition$Sex), main =“Sex”)
barplot(table(attrition$JobInvolvement), main =“JobInvolvement”)
barplot(table(attrition$MaritalStatus), main =“MaritalStatus”)
barplot(table(attrition$OverTime), main =“OverTime”)
barplot(table(attrition$JobSatisfaction), main =“JobSatisfaction”)

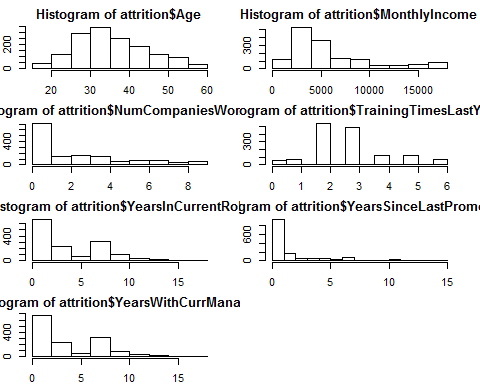
Distribution of Continuous Variables

par(mfrow=c(4,2))
par(mar = rep(2, 4))
hist(attrition$Age)
hist(attrition$MonthlyIncome)
hist(attrition$NumCompaniesWorked)
hist(attrition$TrainingTimesLastYear)
hist(attrition$YearsInCurrentRole)
hist(attrition$YearsSinceLastPromotion)
hist(attrition$YearsWithCurrManager)

Building Predictive Models

Baseline Accuracy

table(attrition$Attrition)

##
##    0           1
## 1233      237

237 out of total 1470 observations left the job. So the baseline accuracy is 1233/1470 = 84%, without building any model. But this naive way would classify all employee churned as non-churn, which defeats the purpose of creating a response plan to reduce employee attrition.

Let’s go ahead and build a model which is more ‘sensitive’ to our business requirement.

Dividing the dataset

Before doing any modeling, let’s divide our data set into training and testing data set to evaluate the performance of our model.

#Dividing the data set into train and test
library(caTools)

## Warning: package ‘caTools’ was built under R version 3.2.4

set.seed(200)
spl = sample.split(attrition$Attrition, SplitRatio = 0.70)

train = subset(attrition, spl == TRUE)
test = subset(attrition, spl == FALSE)

Logistic Regression

Build a logistic regression model using all of the independent variables to predict the dependent variable “Attrition”, and use the training set to build the model.

log = glm(Attrition ~ . , family=“binomial”, data = train)
summary(log)

##
## Call:
## glm(formula = Attrition ~ ., family = “binomial”, data = train)
##
## Deviance Residuals:
##        Min             1Q             Median             3Q                 Max
##     -1.6850     -0.5645      -0.3447           -0.1810          3.5033
##
## Coefficients:
##                                                                                         Estimate Std. Error z value Pr(>|z|)
## (Intercept)                                                                1.090e+00  7.381e-01   1.477 0.139604
## Age                                                                              -3.866e-02  1.349e-02  -2.866 0.004153 **
## BusinessTravelTravel_Frequently                 1.142e+00  4.241e-01   2.694 0.007059 **
## BusinessTravelTravel_Rarely                          7.295e-01  3.908e-01   1.866 0.061973 .
## Satisfaction_level2                                              -8.338e-01  2.980e-01  -2.797 0.005151 **
## Satisfaction_level3                                              -9.093e-01  2.748e-01  -3.309 0.000936 ***
## Satisfaction_level4                                              -1.046e+00  2.741e-01  -3.815 0.000136 ***
## SexMale                                                                     2.936e-01  2.009e-01   1.462 0.143859
## JobInvolvement2                                                 -1.131e+00  3.872e-01  -2.922 0.003479 **
## JobInvolvement3                                                 -1.230e+00  3.611e-01  -3.406 0.000658 ***
## JobInvolvement4                                                 -1.817e+00  5.048e-01  -3.599 0.000319 ***
## JobSatisfaction2                                                   -3.894e-01  2.865e-01  -1.359 0.174200
## JobSatisfaction3                                                   -5.039e-01  2.543e-01  -1.982 0.047528 *
## JobSatisfaction4                                                   -1.213e+00  2.833e-01  -4.283 1.85e-05 ***
## MaritalStatusMarried                                         3.027e-01  2.819e-01   1.074 0.282906
## MaritalStatusSingle                                              1.248e+00  2.794e-01   4.467 7.92e-06 ***
## MonthlyIncome                                                    -1.057e-04  3.583e-05  -2.950 0.003173 **
## NumCompaniesWorked                                   9.840e-02  4.238e-02   2.322 0.020236 *
## OverTimeYes                                                          1.488e+00  1.999e-01   7.445 9.71e-14 ***
## TrainingTimesLastYear                                    -2.074e-01  7.754e-02  -2.675 0.007468 **
## YearsInCurrentRole                                          -4.289e-02  4.534e-02  -0.946 0.344189
## YearsSinceLastPromotion                              1.589e-01  4.250e-02   3.740 0.000184 ***
## YearsWithCurrManager            –                   1.171e-01  4.512e-02  -2.597 0.009417 **
## —
## Signif. codes:           0    ‘***’    0.001   ‘**’    0.01    ‘*’   0.05   ‘.’     0.1    ‘ ‘     1
##
## (Dispersion parameter for binomial family taken to be 1)
##
##                     Null deviance: 909.34  on 1028  degrees of freedom
##                     Residual deviance: 712.27  on 1006  degrees of freedom
##                    AIC: 758.27
##
##                     Number of Fisher Scoring iterations: 6

All the variables are significant, except YearsInCurrentRole and Sex. Anyways, we will keep it in our model.

Making Predictions on test data, with a threshold of 0.5.

predictLog = predict(log, newdata = test, type = “response”)

#Confusion Matrix
table(test$Attrition, predictLog >= 0.5)

##
##             FALSE    TRUE
##   0          366            4
##   1           45             26

(366+26)/(nrow(test))      #Accuracy 0.89

## [1] 0.8888889

26/71                                      # Sensitivity 0.37

## [1] 0.3661972

Our accuracy has increased form Baseline Accuracy of 83% to 89%. However, that’s not much relevant. What’s important is that our sensitivity has gone leaps and bounds from 0 to 37%.

Area Under the Curve (AUC) for the model on the test data

library(ROCR)

## Loading required package: gplots

##
## Attaching package: ‘gplots’

## The following object is masked from ‘package:stats’:
##
##     lowess

ROCRlog = prediction(predictLog, test$Attrition)
as.numeric(performance(ROCRlog, “auc”)@y.values)

## [1] 0.9018272

The AUC comes out to be 0.90 – indicating high accuracy.

CART Model

The logistic regression model gives us high accuracy, as well as significance of the variables. But there is a limitation. It is not immediately clear which variables are more important than the others, especially due to the large number of categorical variables in this problem.

Let us now build a classification tree for this model. Using the same training set, fit a CART model, and plot the tree.

#CART Model
library(rpart)
library(rpart.plot)

Tree = rpart(Attrition ~ ., method=“class”, data = train)
prp(Tree)

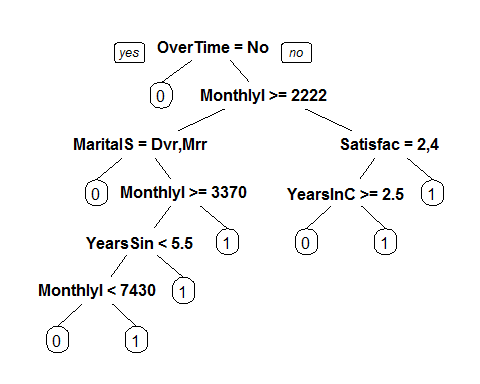
The Variable which the Tree Splits uupon in the first level is ‘OverTime’, followed by ‘MonthlyIncome’, indicating these are the most important variables.

Accuracy of the model on testing data set

PredictCART = predict(Tree, newdata = test, type = “class”)
table(test$Attrition, PredictCART)

##            PredictCART
##                0             1
##   0        358          12
##   1          51           20

(358+20)/nrow(test) #Accuracy ~ 86%

## [1] 0.8571429

20/71                             #Sensitivity ~ 28%

## [1] 0.2816901

AUC of the model

library(ROCR)
predictTestCART = predict(Tree, newdata = test)
predictTestCART = predictTestCART[,2]
#Compute the AUC:
ROCRCART = prediction(predictTestCART, test$Attrition)
as.numeric(performance(ROCRCART, “auc”)@y.values)

## [1] 0.7009326

Interpretation

We see that even though CART model beats the Baseline method, it underperforms the Logistic Regression model. This highlights a very regular phenomenon when comparing CART and logistic regression. CART often performs a little worse than logistic regression in out-of-sample accuracy. However, as is the case here, the CART model is often much simpler to describe and understand.

Random Forest Model

Finally, let’s try build a Random Forest Model.

library(randomForest)

## randomForest 4.6-12

## Type rfNews() to see new features/changes/bug fixes.

set.seed(100)
rf = randomForest(Attrition ~ ., data=train)

#make predictions
predictRF = predict(rf, newdata=test)
table(test$Attrition, predictRF)

##         predictRF
##            0          1
##   0    366       4
##   1      57       14

380/nrow(test)        #Accuracy ~ 86%

## [1] 0.861678

14/71                           #Sensitivity ~ 19.7%

## [1] 0.1971831

The accuracy is better than the CART Model but lower than the Logistic Regression Model.

Understanding Important Variables in Random Forest Model

One way of understanding this is to look at he number of times, aggregated over all of the trees in the random forest model,that a certain variable is selected for a split. This can be done using the following code:

#Method 1
vu = varUsed(rf, count=TRUE)
vusorted = sort(vu, decreasing = FALSE, index.return = TRUE)
dotchart(vusorted$x, names(rf$forest$xlevels[vusorted$ix]))

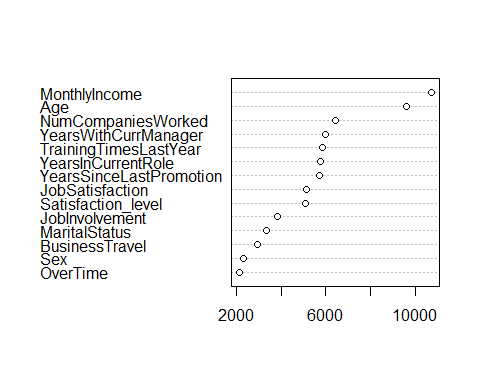
We can see that MonthlyIncome and Age Variables are used significantly more than the other variables.

Method 2

A different metric we can look at is related to “impurity”, which measures how homogenous each bucket or leaf of the tree is. To compute this metric, run the following command in R

varImpPlot(rf)

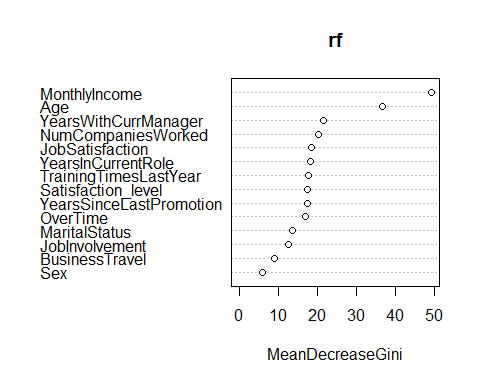
Conclusion – The Advantage of Analytics

In the absence of predictive modeling, we would have taken the naïve approach of predicting the majority of outcomes as the predictions which would have meant we would have labeled all employees as ‘Non Churner’. This would have defeated the entire purpose of controlling employee churn. Using various predictive modeling techniques, the organization is not just able to conveniently beat the baseline model but also predict with increased accuracy which employees have higher probability of leaving the organization.

Action Plan

Finally the organisation can look at the predictions and score the employees basis their probability of leaving the organization and accordingly,develop retention strategies.

End Notes

Please note that this is an introduction to HR Analytics using Predictive modeling. There are various other techniques which can be used to carry out this exercise,which was beyond the scope of this article. Also, even the models which have been constructed could have been improved by fine tuning various parameters. However, these have been not considered to keep the explanation simpler and non-technical.

Author: Vikash Singh

Profile: Seasoned Decision Scientist with over 11 years of experience in Data Science, Business Analytics, Business Strategy & Planning.